PATRICIA TRIE: A PREDESTINED BLOCKCHAIN THING
If you spend time learning blockchain technology, certain terms keep pondering and you start to familiar with it. “ Merkle Tree” and “ Patricia Trie” are among the terms in particular that seem to pop every now and again. Well, quite essential parts of the blockchain thing. Fear not, dear readers, you’ll eventually gather the concept as I am going to keep things simpler.
To brief, Trie is a data structure used in applications like search engines and natural language processing tools involving extensive string processing & retrieval operations. In the Ethereum blockchain, Merkle-Patricia Trie is used for data representation within a block. We’ll see the symphony of Patricia Trie and blockchain in the soon-coming read.
However, to get started, this article reads you the data structure fondly called Patricia Trie- an inevitable blockchain thing. If you have missed reading on Merkle Tree, wanna know about it, read here. You might do a quick read also expand your Merkle Tree pieces of content here.
So before we proceed, let’s clear it off
Is it Trie or Tree?
Is it that we misspell it? No……
The trie (pronounced “try”) is widely used for storing string data sets. Though it was first introduced by Rene de la Briandais in 1959, the term “trie” was later coined by Edward Fredkin, derived from the middle syllable of the word “retrieval.” (It is said that Fredkin pronounced it the same as “tree,” but it was changed to “trie” to avoid confusion.)
Let’s get back to the topic.
Trie as above- mentioned is a tree-like data structure. Here, the root node stores nothing. Edges are labeled with letters and a path from the root to the node represents a string. The nodes come with an indicator, which indicates whether that node represents the end of a string. Our agenda is to make the operation- data reTRIEval faster.
Now it’s clear where we got the word Trie from. Right????
In our example, we have marked such nodes. All other nodes are for branching purposes only and do not store any actual data. Let us see an example.
Initially, the trie has only a root, which is empty. Now…
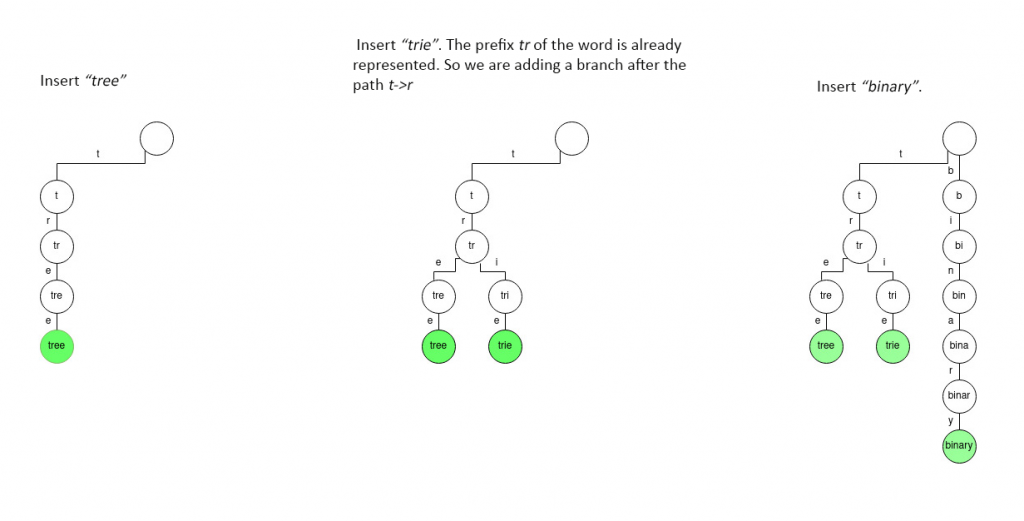
As you see, every node except the root node represents a prefix of a string. Therefore, giving trie another name, “prefix-tree”. Each branch represents a letter of the key. If we are constructing a trie for representing words in English, the maximum number of branches for a node will be 26, one for each letter. If we are dealing with binary strings, the number of branches will be 2, representing 0 and 1.
Searching for a string in a trie is very simple. Just start moving down the tree from the root node, selecting the branches based on the characters in the string. If we find a path that represents the sequence of characters in the search string, check whether the node at the end of the path is marked. If we get stuck at some node or reach an unmarked node at the end of the path, it is assumed that the search is unsuccessful.
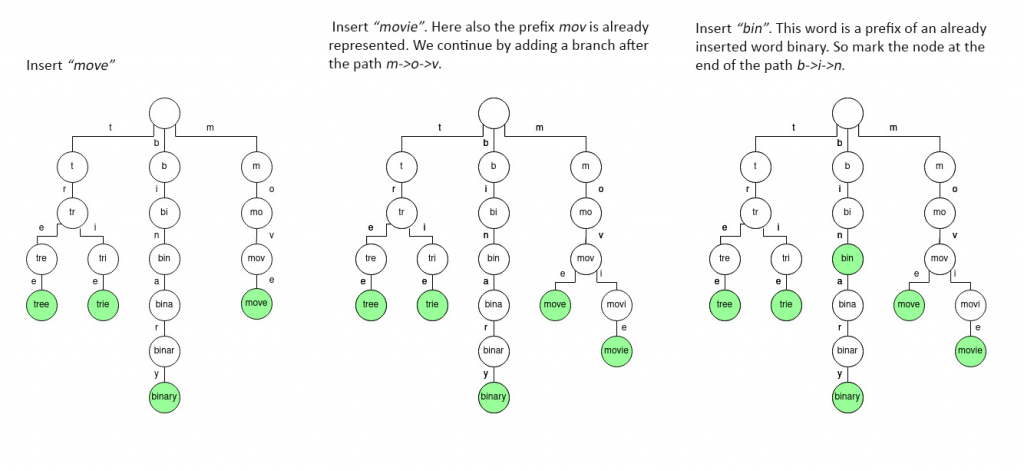
Though the trie representation allows faster search operations, the space requirement is high. We have to store a big tree with too many nodes and too many edges. However, there is a technique to compress the trie.
Look at the previous example.
The majority of the nodes have just one child. Should we really construct a separate node for representing them ?. If we can combine these nodes we can reduce the size of the tree. This is the basic idea behind Patricia Trie.
Patricia Trie
The concept of Patricia-Practical Algorithm To Retrieve Information Coded In Alphanumeric was introduced in the late 1960s by Donald R. Morrison. The actual representation of Patricia Trie is complicated. A simple explanation may be found here. Patricia Trie is found in different variations. For now, we’ll discuss a simple version of Patricia Trie which can be related to its application in the blockchain.
In a Patricia Trie, if a parent node has only a single child node, they will be combined. This is done to compress long paths without any branches into single edges. Finally, we get a trie where every node has at least two branches as shown below.
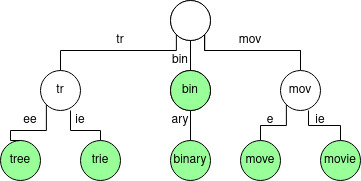
Edges are labeled with single characters or a sequence of characters. The branches are chosen based on a prefix of a string rather than a letter in the string. In search operations, character by character comparisons is replaced by string comparisons which reduce the number of comparisons required.
For a better understanding of trie’s advantages and applications, we first need to understand trie’s representation in detail.
Patricia Trie for (key, value) pairs
Tries are not limited to string representations. They can be used to represent (key, value) pairs, where we have a list of keys and a value associated with each key. Keys are strings represented by the trie and the value will be stored in the node which is at the end of a key path.
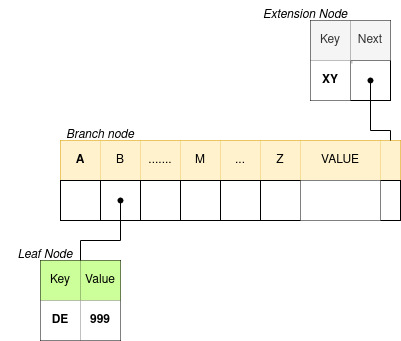
In a Patricia tree, we have three types of nodes
- Branch Node: A node that has more than one child node. It stores links to child nodes.
- Extension Node: A non-leaf node that represents a sequence of nodes that has only one child. It stores a key value that represents the combined nodes, and a link to the next node.
- Leaf Node or Value Node: It is similar to an extension node. But instead of the link, it stores a value.
For example, below is an example representation of nodes of a Patricia trie. It shows the mapping (XYBDE, 999)

We will understand it based on an example. Let us create a key-value mapping for the strings in our previous example.
(BIN, 10) (BINARY, 8) (MOVE, 30) (MOVIE, 55) (TREE, 20) (TRIE, 48)
The final Patricia trie for the above data set looks like below.
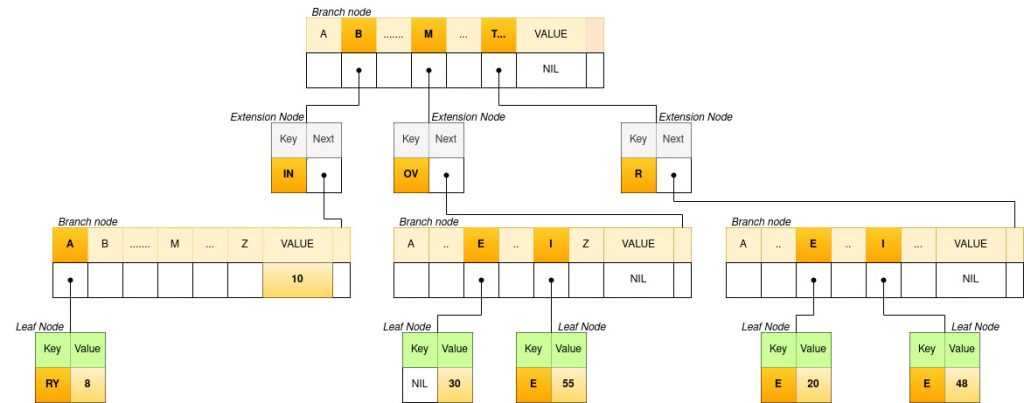
Amused seeing the diagram?
Don’t worry, we’ll decode it.
In our set of keys, the first letter of a key can be B or M, or T. So the main branch node has links for each of them.
After ‘B’, we have a common prefix “IN”. There is an extension node combining the nodes for I and N. The extension node has a field that points to the next branch node. Since BIN is a key whose value is 10, insert 10 to the value field of the branch node (end node of the path BIN). Next, we need to represent the key BINARY. From the branch node, create a link for A, which connects a leaf node with key RY. The value of the key BINARY will be stored in the leaf node.
In the case of the keys MOVE and MOVIE, the extension node for the common prefix MOV is created like the previous case. From the branch node, there is a link from E pointing to the leaf node of MOVE and a link from I pointing to the leaf node for MOVIE. The leaf node for MOVE is at the end of path MOVE, so the key field is left empty and the value is stored in it.
The nodes for TRIE and TREE are also constructed similarly. A branch node is created at the end of the common prefix TR. It has links for E of TREE, and I of TRIE. Finally, the leaf nodes store the value for each key.
Searching for a key is the same as before. Compare the links and key values at each node with the characters in the search key. At the end of the path, if you reach a node that stores a value, the search is successful. If you get stuck at some node or if the node at the end of the path does not have a value stored, the search is unsuccessful.
To conclude, the implementation of Patricia Trie is complicated, however, it is credited with many advantages. It acts as a useful data structure when it comes to applications that need to store a large number of key-value pairs. When compared to standard trie representation, the size of Patricia Trie is small. Searching and retrieval operations can be performed faster. Patricia Tries are blockchain-friendly as they can be used to “prove” the authenticity of a large amount of data, without getting it stored anywhere.
